Introduction to scalar quantization
Most embedding models output vector values. While this provides the highest fidelity, it is wasteful given the information that is actually important in the vector. Within a given data set, embeddings never require all 2 billion options for each individual dimension. This is especially true on higher dimensional vectors (e.g. 386 dimensions and higher). Quantization allows for vectors to be encoded in a lossy manner, thus reducing fidelity slightly with huge space savings.
Understanding buckets in scalar quantization
Scalar quantization takes each vector dimension and buckets them into some smaller data type. For the rest of the blog, we will assume quantizing values into . To bucket values accurately, it isn't as simple as rounding the floating point values to the nearest integer. Many models output vectors that have dimensions continuously on the range . So, two different vector values 0.123 and 0.321 could both be rounded down to 0. Ultimately, a vector would only use 2 of its 255 available buckets in , losing too much information.
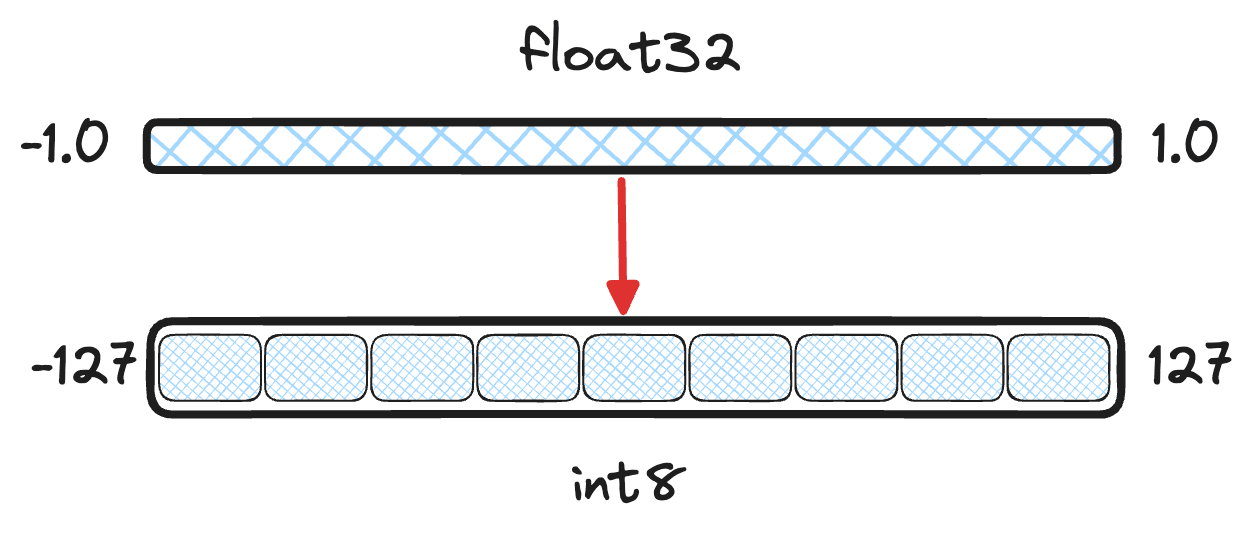
Figure 1: Illustration of quantization goals, bucketing continuous values from to into discrete values.
The math behind the numerical transformation isn't too complicated. Since we can calculate the minimum and maximum values for the floating point range, we can use min-max normalization and then linearly shift the values.
Figure 2: Equations for transforming between and . Note, these are lossy transformations and not exact. In the following examples, we are only using positive values within int8. This aligns with the Lucene implementation.
The role of statistics in scalar quantization
A quantile is a slice of a distribution that contains a certain percentage of the values. So, for example, it may be that of our floating point values are between instead of the true minimum and maximum values of . Any values less than -0.75 and greater than 0.86 are considered outliers. If you include outliers when attempting to quantize results, you will have fewer available buckets for your most common values. And fewer buckets can mean less accuracy and thus greater loss of information.
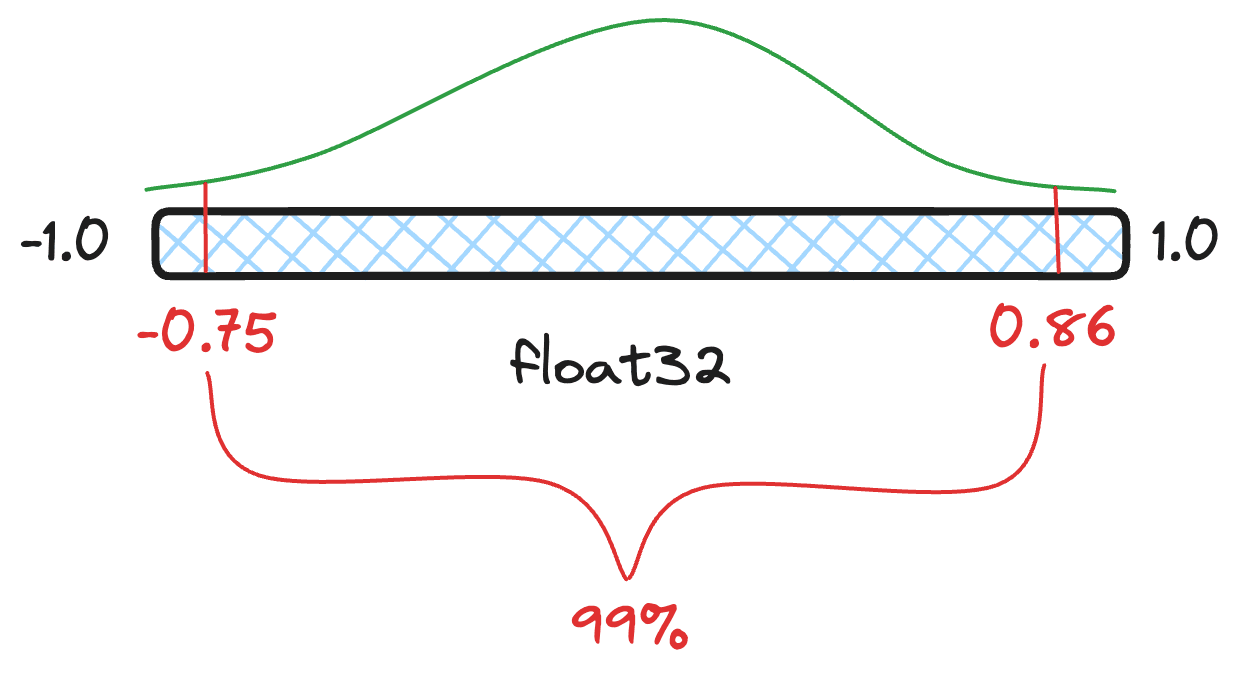
Figure 3: Illustration of the confidence interval and the individual quantile values. of all values fall within the range .
This is all well and good, but now that we know how to quantize values, how can we actually calculate distances between two quantized vectors? Is it as simple as a regular dot_product?
The role of algebra in scalar quantization
We are still missing one vital piece, how do we calculate the distance between two quantized vectors. While we haven't shied away from math yet in this blog, we are about to do a bunch more. Time to break out your pencils and try to remember polynomials and basic algebra.
The basic requirement for dot_product and cosine similarity is being able to multiply floating point values together and sum up their results. We already know how to transform between and values, so what does multiplication look like with our transformations?
We can then expand this multiplication and to simplify we will substitute for .
What makes this even more interesting, is that only one part of this equation requires both values at the same time. However, dot_product isn't just two floats being multiplied, but all the floats for each dimension of the vector. With vector dimension count in hand, all the following can be pre-calculated at query time and storage time.
is just and can be stored as a single float value.
and can be pre-calculated and stored as a single float value or calculated once at query time.
can be pre-calculated and stored as a single float value.
Of all this:
The only calculation required for dot_product is just with some pre-calculated values combined with the result.
Ensuring accuracy in quantization
So, how is this accurate at all? Aren't we losing information by quantizing? Yes, we are, but quantization takes advantage of the fact that we don't need all the information. For learned embeddings models, the distributions of the various dimensions usually don't have fat-tails. This means they are localized and fairly consistent. Additionaly, the error introduced per dimension via quantization is independent. Meaning, the error cancels out for our typical vector operations like dot_product.
Conclusion
Whew, that was a ton to cover. But now you have a good grasp of the technical benefits of quantization, the math behind it, and how you can calculate the distances between vectors while accounting for the linear transformation. Look next at how we implemented this in Lucene and some of the unique challenges and benefits available there.